Albert Einstein provided physicists with a spectacularly successful theory of spacetime on very large, astronomical scales. This masterwork -- general relativity -- envisions spacetime as being completely flat in the absence of matter or energy. The theory departs from Newton's ideas, however, once masses are introduced. While Newton thought of space and time as being absolute and unchanging entities, Einstein proposed that masses, such as those of a galaxy or the Sun, cause spacetime to warp, much as a person standing on a trampoline causes it to sag (Figure 1). But Einstein went even one step further. General relativity asserts that the warping of spacetime actually is gravity! In other words, the Earth's orbit around the Sun is not shaped by some mysterious "force" acting across vast space. Rather, the Earth simply follows the shortest path in the warped spacetime caused by the sun's presence. To quote physicist John Archibald Wheeler: "Matter tells space how to curve and space tells matter how to move."
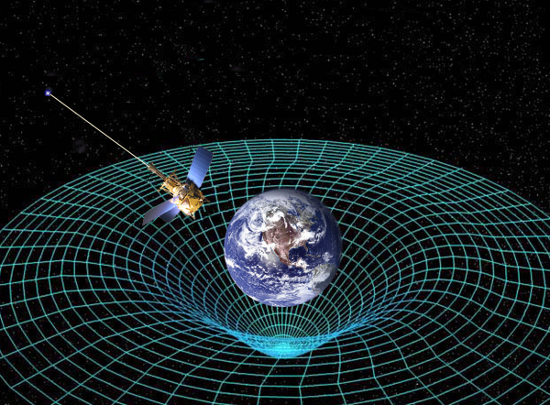
Figure 1. Artist's concept of warped spacetime, with NASA's mission Gravity Probe B.
You'll notice that the basic premise of general relativity is that spacetime is a smooth, gently curving, geometrical entity that allows us to follow all of its matter-driven undulations. The situation is utterly different when we observe the extremely small, subatomic scale. That is the realm of quantum mechanics -- a theory in which probability, rather than determinism, reigns supreme. Quantum mechanics is incredibly successful in the subatomic world. So much so that we can calculate the strength of the tiny magnet associated with the electron, and the theoretical value agrees with the experimentally measured one to within eight parts per trillion!
In order to unify the theory of the large -- general relativity -- with the theory of the small -- quantum mechanics -- physicists had to examine the properties of spacetime on the tiniest scales. And here is where the problem arose. In quantum mechanics, the uncertainty principle implies that the smaller the region of spacetime we observe, the larger the fluctuations in it. Even without any matter or energy, rather than being placid, spacetime undergoes a quantum frenzy; the narrower our focus, the more the fluctuations become increasingly violent. Given that the warping of spacetime is gravity, all hope of making any sensible predictions is lost. In fact, by the time one gets to the extremely tiny scale of 10 centimeter (1 at the 33rd decimal place; known as the Planck scale), all hell breaks loose, and calculations simply yield infinity at every step -- a sure sign of a theory gone completely awry. The effect can be visualized using portraits of the incredible artist Chuck Close as an example. When seen from a distance, these portraits look extremely smooth and astoundingly accurate and detailed (e.g., this photo). From up close, however, one discovers that many of them are composed of richly and wildly painted grid squares (e.g., this painting).
The bottom line is clear. General relativity provides an accurate description of spacetime on cosmic scales, but it becomes inadequate on subatomic scales. Should we worry about this? Or can we simply live happily with two separate theories, one applying to the universe at large, and the other to subatomic physics? I shall attempt to address this question in the next blog posting.
NOTE: Einstein has taught us that time is a relative entity. In particular, time passes more slowly for an observer in motion (special relativity), or in a stronger gravity (general relativity). Consequently, the Hubble Space Telescope would be a little "younger" than a similar telescope on the ground (such as the one recently donated by the military to NASA). Based on Hubble's speed in orbit (of about 17,500 miles per hour), the effect would amount to only a few tens of billionths of a second over Hubble's lifetime of 22 years. The fact that gravity at Hubble's orbit is weaker than on the ground results in an opposite trend (Hubble being "older"), but since this effect is considerably smaller than the one due to the speed, the net result is Hubble being "younger."