Mathematicians consider the invention (or discovery, depending on your point of view) of zero as one of the most important intellectual advances humans have ever made. Why? Isn't zero just sheer nothingness? Nothing could be further from the truth.
Zero is not only a concept of nothingness, which allows us to do arithmetic well and to algebraically define negative numbers, but it is also an important place-holding device. In that role, zero enables our base-10 number system to work, so that the same 10 numerals can be used over and over again, at different positions in a number. This is exactly what makes our number system so efficient and powerful. Without that little zero we would be stuck in the Middle Ages!
The Roman system, for example, which preceded our number system and surprisingly remained in use in Europe until as late as the thirteenth century, employed Latin letters for quantities (I for 1, X for 10, L for 50, C for 100, M for 1,000). These letters had to be repeated, for example writing MMMCCCLXXIII for the number 3,373. We see that in our system the same numeral 3 is used in three different places, allowing for economy and ease of notation. None of the Latin letters could be repeated in different roles. In our number system, it is the zero that enables the system to work: Thus, a 5 in the units location is a 5; but the same symbol in the tens location makes it a 50 -- if we can also use a zero as an empty place-holder for the units.
The millennia-old Babylonian system, for example, which predated the Greco-Roman letter-based number system, used base-60 with no place-holding zero. Hence, the difference between 62 and 3602 (where 3600 is the next-up power of 60) had to be guessed from the context. Our number system, using a much smaller base, and employing a special symbol for zero, derives its immense power and usefulness through this place-holding zero. When we also consider the fact that everything we do with a computer (or cellular phone, GPS, or anything electronic) is controlled by strings of zeros and ones, it becomes clear just how great an invention this was.
So who invented it?
Until 1930, many scholars in the West believed that the zero was either a European or an Arab invention. A highly polemical academic argument was raging at the time, where British scholars, among them G. R. Kaye, who published much about it, mounted strong attacks against the hypothesis that the zero was an Indian invention. The oldest known zero at that time was indeed in India, at the Chatur-bujha temple in the city of Gwalior. But it was dated to the mid-ninth century, an era that coincided with the Arab Caliphate. Thus Kaye's claim that zero was invented in the West and came to India through Arab traders could not be defeated using the Gwalior zero.
But then in 1931, the French archaeologist Georges Cœdès published an article (see reference below) that demolished Kaye's theory. In it, he proved definitively that the zero was an Eastern (and perhaps Cambodian, although he viewed Cambodia an "Indianized" civilization) invention. Cœdès based his argument on an amazing discovery. Early in the twentieth century, an inscription was discovered on a stone slab in the ruins of a seventh-century temple in a place called Sambor on Mekong, in Cambodia. Cœdès gave this inscription the identifier K-127. He was an expert philologist and translated the inscription from Old Khmer. It begins:
Chaka parigraha 605 pankami roc...
Translated: The Chaka era has reached 605 on the fifth day of the waning moon...
The zero in the number 605 is the earliest zero we have ever found. We know that the Chaka era began in AD 78, so the year of this inscription in our calendar is 605 + 78 = AD 683. Since this time predates the Arab empire, as well as the Gwalior zero, by two centuries, Cœdès was able to prove that the zero is, in fact, an Eastern invention. It is believed to have come to the West via Arab traders and was popularized in Europe through the work of Fibonacci (of the famous sequence of numbers), published in 1202.
For a time, inscription K-127 was kept in the Cambodian National Museum in Phnom Penh. But during the Khmer Rouge reign of terror, while killing more than 1.7 million of their own people, Pol Pot and his henchmen also stole or destroyed close to 10,000 artifacts -- and this priceless inscription's whereabouts were unknown.
I felt that it was very important for the history of science that the oldest zero ever found be rediscovered. With the generous support of a grant from the Alfred P. Sloan Foundation in New York, I headed for Cambodia in December 2012. I had very little going for me, and a mathematician friend, Bill Casselman of the University of British Columbia, who had worked on the Gwalior zero, told me that a visitor from Cambodia had informed him that too much had been destroyed by the Khmer Rouge to assume that K-127 still existed.
After spending time in the field and talking with people I had hoped might be able to help, I decided to appeal directly to the Cambodian Government. His Excellency Hab Touch, Director General of the Ministry of Culture and Fine Arts, provided the key to my ultimate success. While extremely busy directing the management of Cambodia's 4,000 ancient temples (of which the famous Angkor Wat is one), he still found time to help me. He informed me that on November 22, 1969, K-127 was moved to Angkor Conservation near the town of Siem Reap, home of Angkor Wat. The bad news was that in a resurgence of their violence as late as 1990, the Khmer Rouge had plundered this location. But he offered to have his people at Angkor Conservation help me look there.
I traveled to the compound called Angkor Conservation, in a field outside Siem Reap, on the way to the Angkor Wat complex. There, I searched among literally thousands of artifacts lying on the ground in large sheds. I don't know how -- but on January 2, 2013, late in the afternoon, I finally found K-127! I was elated. My wife, Debra, took several photographs of the inscription. Below is the only picture (with a few others my wife took) that exists of this priceless find. Cœdès had used only a pencil-rubbing, and never had a photograph. The dot in the center, to the right of the inverted-9-looking sign (which is 6 in Old Khmer) is the oldest zero ever discovered. His Excellency Hab Touch has promised me to bring K-127 back to the Cambodian National Museum in Phnom Penh, where it belongs, and where, hopefully, everyone would soon be able to see it.
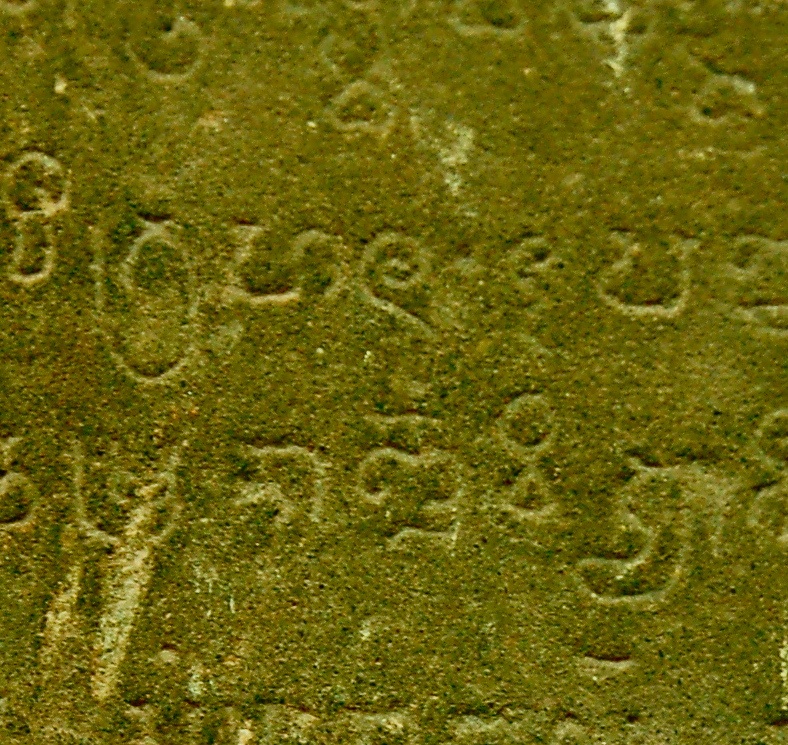
Photo Credit: Debra Gross Aczel
References:
Cœdès, Georges, "A propos de l'origine des chiffres arabes," Bulletin of the School of Oriental Studies, University of London, Vol. 6, No. 2, 1931, pp. 323-328.
Diller, Anthony, "New Zeros and Old Khmer," The Mon-Khmer Studies Journal, Vol. 25, 1996, pp. 125-132.
Ifrah, Georges. The Universal History of Numbers. New York: Wiley, 2000.