
Game theory? No, I'm not about to tell you that a hotel on Marvin Gardens will earn you more Monopoly cash than a hotel on Park Place. Game theory is a rigorous and often probabilistic approach to strategic problem solving, and one of the best models for examining human conflict and cooperation. Now, don't be anxious if that was a mouthful; it's a lot simpler than it sounds.
For decades since a breakthrough 1928 paper by the Hungarian polymath John von Neumann, mathematicians have been manufacturing the game theory puzzle pieces and economists have been joining them together. More recently, political scientists, evolutionary biologists, and even sports statisticians have gotten in on the fun. However, with no more than a little logical inference and number comparison, we'll be able to make meaningful predictions about virtually any interactive system.
Let's imagine you're a newspaper journalist and you've just been selected to cover a lucrative modern art auction at Sotheby's. The pièce de résistance today: a broad color-field work by the abstract expressionist Mark Rothko. And while you are stirred by the artist's intense, powerful brushstrokes, you cannot contain your amazement at the verbal volley of CEO salaries ringing in your ears. (Note: "No. 1 (Royal Red and Blue)" by Mark Rothko was sold at Sotheby's for $67 million in November 2012)
But how do the bidders decide whether or not to cast a higher offer? Each time our wealthy Mexican magnate (let's call him Carlos) increases his bid, he's faced with one of two outcomes; he either wins the auction or his opponent Ekatarina tops him and the bidding continues.
As a rational, self-interested actor, Carlos is seeking to maximize his utility: we can think of this as the satisfaction he derives from the whole endeavor. Of course, in this case, his satisfaction is the ability to go home with a great piece of art at a bargain price. If Carlos personally values Rothko's painting at price V, he will only be willing to bid up to price V; any higher and he will endure a loss on the transaction. We'll denote the price the painting actually sells for as P. So we can represent his utility as (V - P) times the probability that he ends the auction with a bid that Ekatarina cannot surpass. Ekatarina is meanwhile performing similar calculations to ensure she doesn't get swindled.
Carlos has pushed the standing bid up to $53 million and the house is hush with anticipation. The auctioneer is preparing to issue his warning to close the deal and our multinational aristocrats are in solemn thought. Let's pause the game and imagine that we've already done the utility calculations so that we can inspect the decision these two are being faced with.
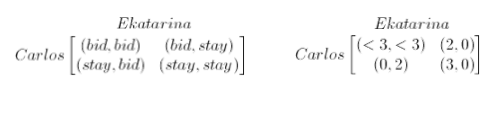
The first table above represents the potential strategies Ekatarina and Carlos can take, while the second table the utilities each one of them receives for those strategies. In both tables, the first element of each ordered pair corresponds to Carlos, while the second corresponds to Ekatarina. So, for example, in (stay, bid), Carlos decides to stay, while Ekatarina decides to bid. Since Carlos stays, the auction ends and he receives 0 utility (since he loses and doesn't get to purchase the painting). Conversely, Ekatarina receives 2 utility since she manages to snag the artwork, presumably valuing it at a price higher than what she pays.
Many games can be solved by just comparing these utility values across rows and columns; however this game is a little more complicated and requires advanced optimization techniques. Incidentally, neither Carlos nor Ekatarina managed to win this particular auction; a mystery telephone bidder called in and took home the striped masterpiece.
So, whether you're a Warhol junkie or a Pollock curator, rest assured that game theory will help you secure something to decorate that empty stretch of wall space between your golden stairwell sconces. So what is in a game? Nothing more than basic human intuition, laid out in such a form that we can examine multiple scenarios at once. Not too bad, huh?