
The recent reports on the disappearance of bee populations have omitted mention of their role in the longest-standing open problem in mathematics, dating from the first millennium B.C.E. and solved in the nick of time (actually with a year to spare; see Scientific American) for the second millennium in 1999. The ancient conjecture, now a theorem, says that the hexagonal honeycomb of Figure 1 provides the most efficient (least-perimeter) way to divide the plane into unit areas. A proof was announced by Thomas Hales in 1999, the same Hales who the year before had proved the 1611 Kepler sphere-packing conjecture, a mere 387 years old. This in turn was on the heels of the celebrated 1995 proof by Princeton mathematician Andrew Wiles of Fermat's 1637 "Last Theorem," similarly a mere 358 years old.

Figure 1. Regular hexagons provide the least-perimeter way to divide the plane into unit areas. Image from wikipedia.org.
Since antiquity, philosophers and honeybees had regarded hexagons as the ideal way to partition the plane into equal areas. The oldest extant record appears in the deathbed epistle of the Roman soldier Marcus Terentius Varro, which contained instructions to his young wife on the care of their farm estate. Varro prized and studied their collection of bees and gave two reasons for the hexagonal shape in their honeycombs: first, that a bee has six feet; second,
the geometricians prove that this hexagon inscribed in a circular figure encloses the greatest amount of space.
Most likely, Varro is referring to work of the Greek mathematician Zenodorus (~200 B.C.E.), who probably did not consider all possible shapes, but just hexagons, triangles, and parallelograms. Nevertheless, I think that the statement counts. Incidentally, Varro's knowledge of bees was not perfect. He also ventured that
they follow their king wherever he goes [emphasis added].
The fact that the leader is not a king but a queen was not discovered until the seventeenth century.
It was shortly after Hales had finished his proof of Kepler's Conjecture that the distinguished physicist Denis Weaire recommended to him this even older Hexagonal Honeycomb Conjecture: "Given its celebrated history, it seems worth a try." Widely believed and often asserted as fact, even by such an eminent mathematician and physicist as Hermann Weyl, it had eluded mathematical proof for millennia. Hales promptly dispatched it in under a year. "In contrast with the years of forced labor that gave the proof of the Kepler Conjecture, I felt as if I had won a lottery." Incidentally, a difficulty with the honeycomb and its symmetry was pointed out in 1994 by Gary Larson.
Long before Hales's proof of the Hexagonal Honeycomb, indeed from antiquity, it was known that among hexagons the regular ones provide the least-perimeter tiling, among triangles the equilateral ones, and among 4-gons squares, as in Figure 2.
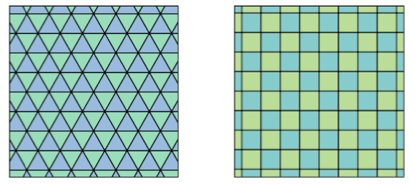
Figure 2. Equilateral triangles and squares provide the least-perimeter tilings by triangles and 4-gons. Images from wikipedia.org.
Still open today, however, is the least-perimeter tiling by pentagons. Regular pentagons cannot be used because they do not fit together to make a tiling, as illustrated in Figure 3.
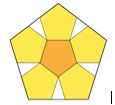
Figure 3. Unfortunately regular pentagons do not fit together to tile the plane. Image from wikipedia.org.
In a forthcoming article in the 2012 Notices of the American Mathematical Society, a joint paper of mine with undergraduate research students (Ping Ngai Chung, Miguel A. Fernandez, Yifei Li, Michael Mara, Isamar Rosa Plata, Niralee Shah, Luis Sordo Vieira, and Elena Wikner) identifies the two leading candidates in Figure 4 and proves them best if all of the pentagons are assumed to be convex, that is, with no indentations. The first, "Cairo" tile, long popular in Cairo, Egypt, has two right angles and three angles of 120 degrees, circumscribed around a circle. The 120-degree angles meet happily in threes; the right angles meet happily in fours. The second, "Prismatic," house-shaped tile also has two right angles and three angles of 120 degrees, but its two right angles are adjacent. It also is circumscribed about a circle. The Cairo and Prismatic tiles have identical perimeter of about 3.86, less than a unit square's (4) but more than the regular pentagon's (about 3.81).
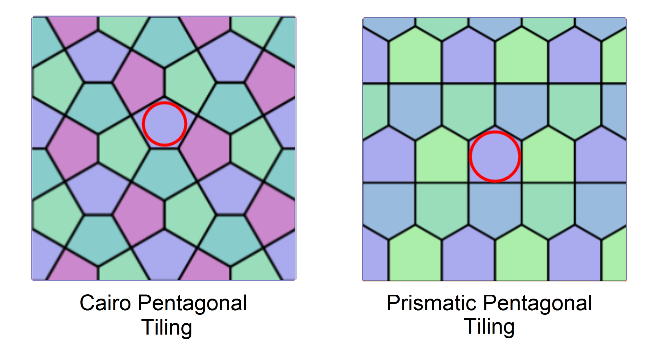
Figure 4. The Cairo and Prismatic pentagon tilings provide least-perimeter tilings of the plane by convex pentagons.
Although no mixtures of convex pentagons can do better, my student colleagues found infinitely many equally good tilings by combining the two tiles as in Figures 5−13, as described by my student colleague Niralee Shah, now a senior at Williams College, in Video 1.
Video 1. Niralee Shah, Williams '12, describes their discovery of infinitely many efficient pentagonal tilings.
The tilings have a variety of symmetries, including some common to wallpaper patterns. The first one, in Figure 5, is due to Marjorie Rice, a housewife who studied tilings as a hobby and made important discoveries.
Figure 5. Cairo-Prismatic tiling by homemaker Marjorie Rice.
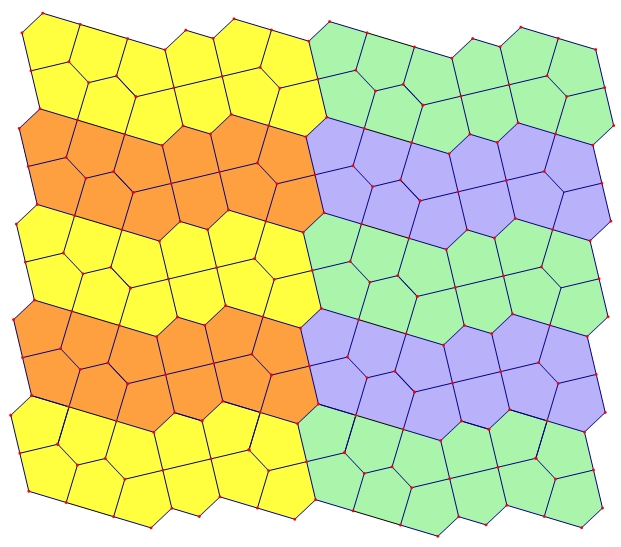
Figure 6. "Sardines" Cairo-Prismatic tiling with wallpaper group p1.
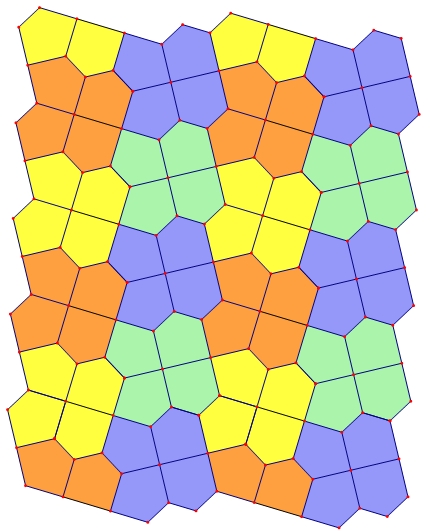
Figure 7. "Stripes" Cairo-Prismatic tiling with wallpaper group p2.
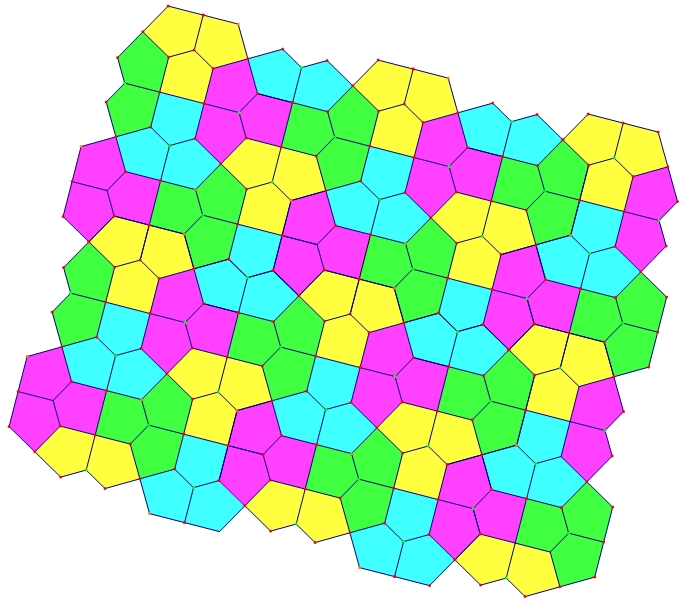
Figure 8. "Pills" Cairo-Prismatic tiling with wallpaper group p4g.
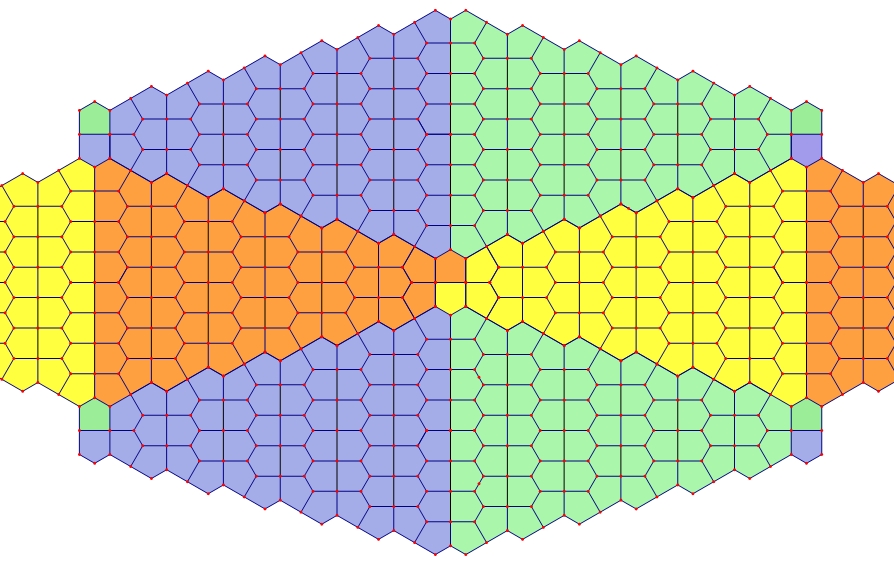
Figure 9. "Christmas Tree" Cairo-Prismatic tiling with wallpaper group cmm.
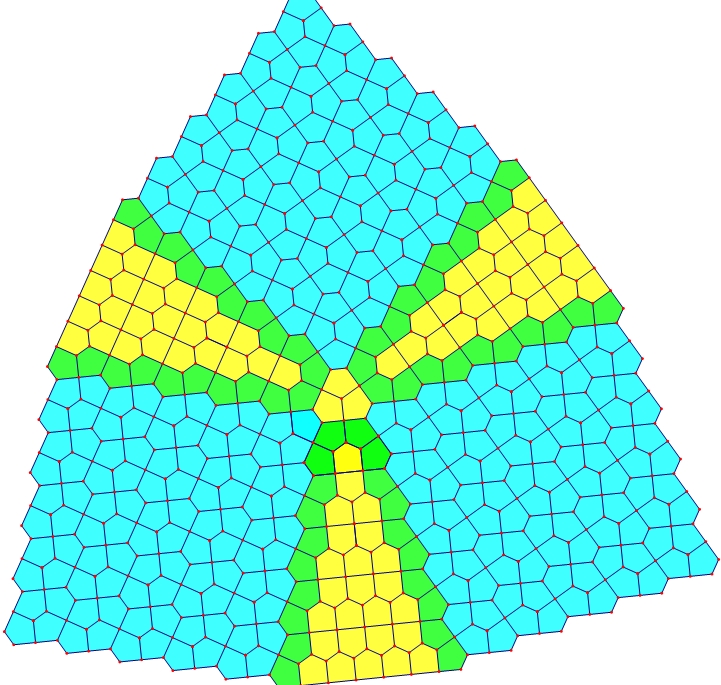
Figure 10. "Windmill" Cairo-Prismatic tiling with dihedral symmetry group D¬¬3.
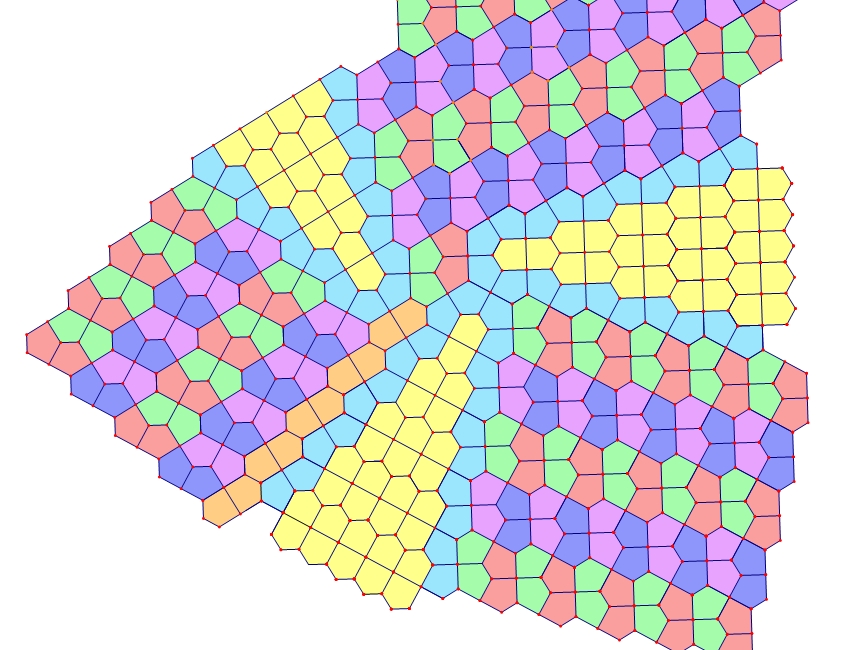
Figure 11. "Chaos" Cairo-Prismatic tiling with no symmetry.
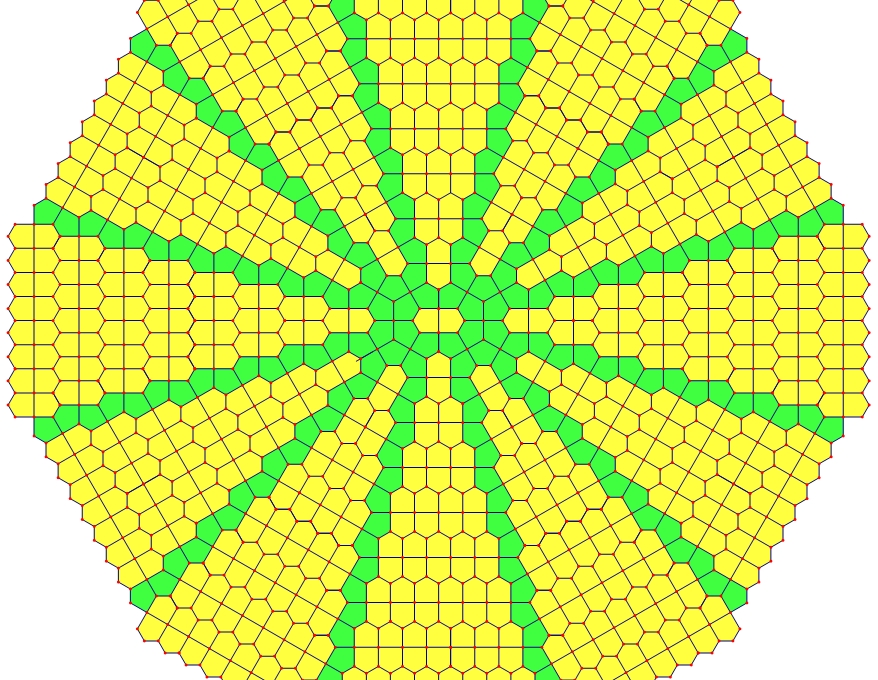
Figure 12. "Plaza" Cairo-Prismatic tiling with dihedral symmetry group D2.

Figure 13. "Bunny" Cairo-Prismatic tiling with dihedral symmetry group D1.
It remains an open question whether one could do better by mixing in some nonconvex pentagons, as described by my student colleague Ping Ngai Chung, now a sophomore at MIT, in Video 2.
Video 2. Ping Ngai Chung, MIT '14, describes the perplexing possibility of more efficient tilings by mixing in some nonconvex pentagons.