Planar (flat) soap bubble clusters seek to enclose, say, N unit areas with the least amount of fencing:
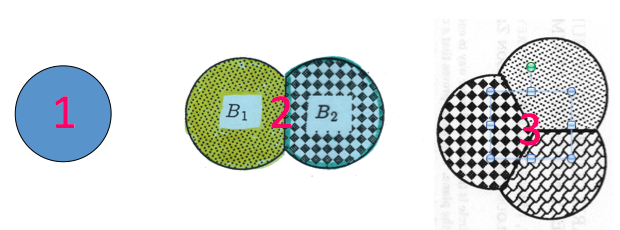
The best single bubble (N=1) is a circle, the best double bubble (N=2) is two overlapping circles with a straight line down the middle, and the best triple bubble (N=3) is three overlapping circles with three separating lines emanating from the center. In 2003 Cox, Graner, et al. computed the following optimal clusters for 3 ≤ N ≤ 42:
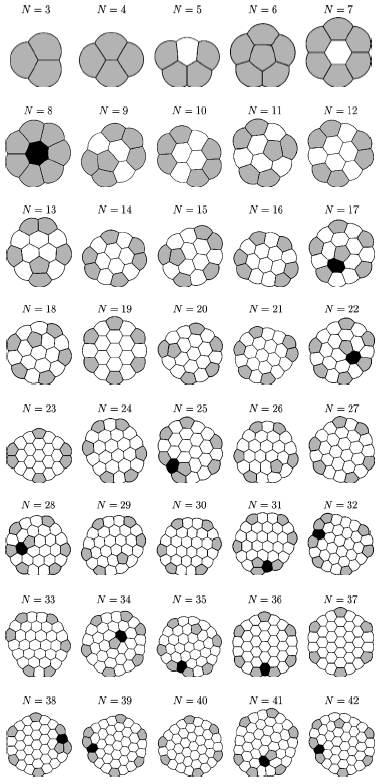
It is hard to see a pattern. Yes, the individual bubbles are becoming hexagonal, the optimal shape for filling the whole plane, as described in our recent post. Most of the interior bubbles have six sides, and most of the boundary bubbles have five sides, but some (colored black) have more sides, and others (colored gray) have fewer sides. Especially focusing on such cases as N = 6, 19, and 37 and larger ones, Cox and Graner conjectured that the whole cluster was becoming hexagonal to accommodate the hexagonal structure from the individual bubbles. I, on the other hand, conjectured that the whole cluster should become round to minimize the perimeter. In March Cox, Sullivan, and I organized a conference, described in our recent post on Soap Bubbles in Scotland. Cox described why he loves such conferences:
We made progress at the conference. After further computations, the next month Cox sent me the following email message:
Date: Wed, 25 Apr 2012
From: Simon Cox
To: Frank Morgan
Subject: large circular clusters
Congratulations Frank!
You win. ...
Simon
For example, for N = 1000, rounding improves the big hexagon:
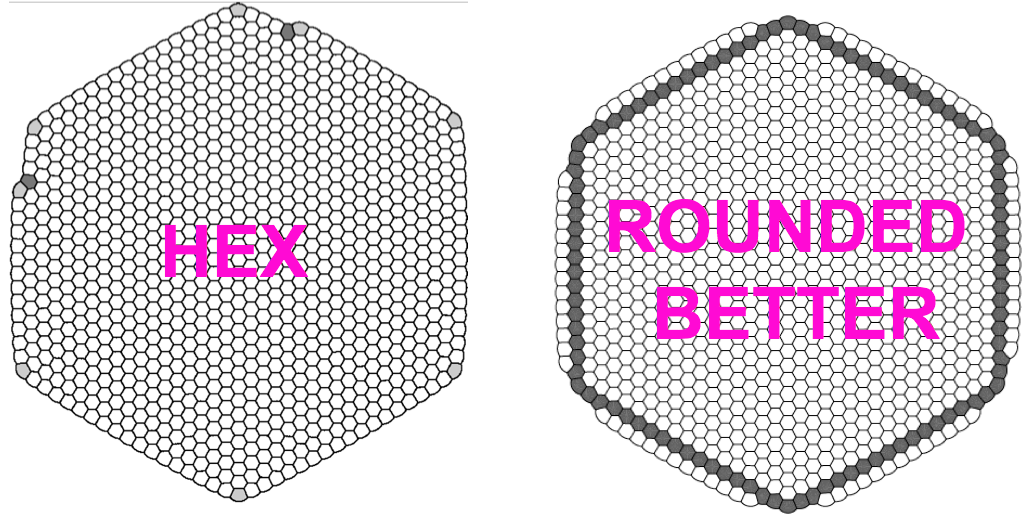
We posted a joint paper with these results on Tuesday. It is not yet clear that the clusters will keep getting rounder, but I think that they will.
Most of these results are just numerical. The only cases mathematically proved optimal are the single, double, and triple bubble (N = 1, 2, 3). A single round circle was proved optimal by Zenodorus about 200 B.C. The double bubble was proved optimal by a group of undergraduate students in 1993. The triple bubble was proved optimal in a Ph.D. thesis by Wichiramala under the supervision of Sullivan at Illinois in 2002. The quadruple bubble remains unproven today.
For more, see my Geometric Measure Theory book.
But can this expectation of a more-rounded, less-hexagonal cluster not just be justified convincingly and almost trivially from an appeal to physical intuition? Minimizing the surface energy of a large bubble cluster surely demands sphericity in the limit that the bubble network is described by a continuous approximation?
For moderately-large N, I conjecture there's a phase transition between various approximations to a straight edge. The optimal arrangement should be a configuration with six-fold symmetry and regions of the different phases with lengths that correspond roughly to their respective energies.
Honeybees, those busy little experimentalist, (László Fejes Tóth showed us that they weren't mathematicians) end up with pentagons in the upper and lower rows. It's easy to place bubbles on a surface in that same pattern ... it feels natural.
Why?
Why are some 5,6,or multiple sided?