
In the current, observationally successful picture of how the Universe developed, there is an origami analogy that is helpful in understanding the formation of the "cosmic web" arrangement of galaxies. The cosmic web is the cellular, foam-like arrangement of galaxies in the Universe; they line the edges of vast voids.
In Einstein's theory of general relativity, gravity comes about through the distortion that matter and energy produce in a four-dimensional spacetime "sheet." Gravity also causes another kind of sheet that pervades space to distort and fold: the three-dimensional cosmological "origami" sheet of dark matter.
As we know from observations of the microwave sky, just after the Big Bang, the dark-matter sheet was very evenly laid out, i.e., the density varied little from point to point in space. However, there were tiny density fluctuations, ripples imprinted on this sheet (quantum fluctuations that "inflated" to macroscopic size in the first instant of time, we suspect, but that's another story).
In dense regions where the sheet has contracted a bit, the sheet contracts and bunches up, eventually forming structures like galaxies. Likewise, less-dense regions get evacuated; there, the sheet stretches out, to form voids between galaxies. The rich get richer, and the poor get poorer. This process is shown in the first figure, an animated sheet of particles from a computer simulation. The colors correspond to the initial, tiny density fluctuations imprinted on the sheet initially, which tell it where to stretch out (blue), and where to bunch together and fold (red). Here, to clarify the motions, the expansion of the Universe has been subtracted out.
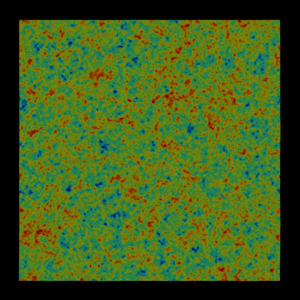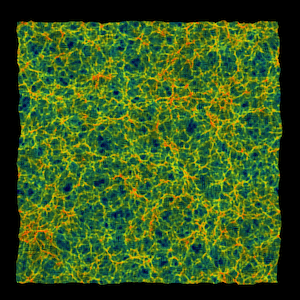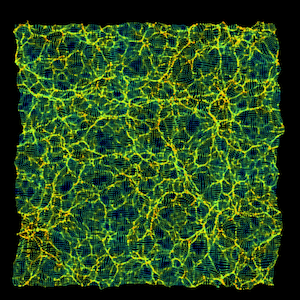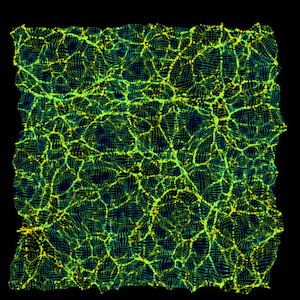
The stretching and bunching-together that gravity produces in the dark-matter sheet, drawn from a computer simulation of dark-matter clustering in the Universe. The physical size of the sheet here is huge, about a billion light-years. One of the smaller clumps that forms would correspond to our Milky Way galaxy.
There is another important piece of physics here: the "collisionless" property that dark-matter particles have. That is, they can blithely pass right through each other. Ordinary matter does care if it hits other bits of matter; a falling apple stops if it hits the ground (or Newton's head). But a dark-matter apple would pass right through. (Never mind that dark matter cannot interact electromagnetically to make things like apples.)
The origami analogy may (or may not) make a bit more sense if we view the 3D sheet of dark-matter in a six-dimensional, position-velocity "phase" space. In this space, each particle of matter is plotted with its usual three position coordinates, but also additionally the three coordinates of its velocity. In this 6D phase space, dark matter's collisionlessness ensures that its sheet can never cross itself, or tear, just like a 2D paper-origami sheet is not allowed to cross itself or tear when it folds up. We know that dark matter is collisionless because otherwise, the Universe would not be able to construct structures with nearly as much richness as we observe around us. The creases, folds, or "caustics," as they are called in cosmology, are physically important because they mark the edges of structures like galaxies (technically, the dark matter "halos" around them), and filaments of galaxies.
The analogy to origami only goes so far, though. First, the cosmological origami sheet is stretchy, unlike in paper origami. Second, the cosmological sheet is three-dimensional, folding up in six dimensions, unlike 2D paper-origami sheets that fold up in 3D.
In the below, very schematic illustration of galaxy formation, the left panels depict the folding up of a single galaxy. On the right, we see a hexagonal network of six galaxies folding up. The result is a design that is squashed flat in 2 dimensions, just as a folded-up dark-matter sheet is more easily visualized after it is flattened back down to the 3 position dimensions.
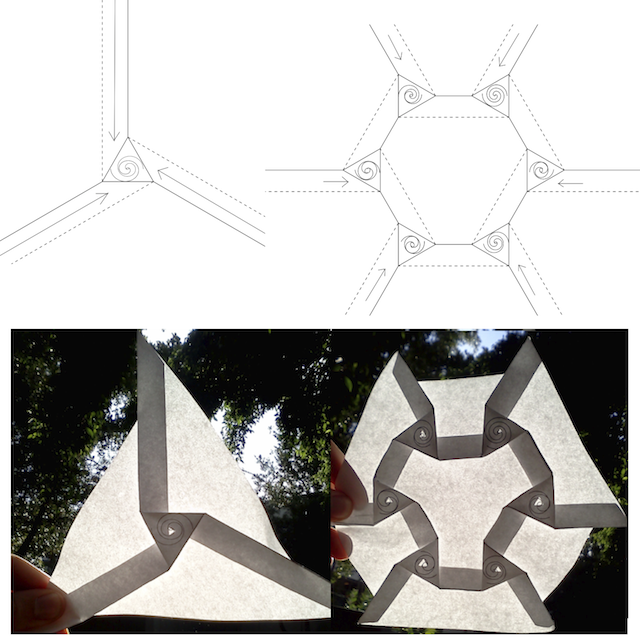
Schematic, fold-your-own paper galaxies.
This origami viewpoint helps to explain why galaxies tend to form with filaments poking out of them. Without stretching the paper, in fact it is impossible to form a compact knot in paper origami without producing filamentary folds at the same time.
Such an origami viewpoint also helps to understand the growth of complexity; the complexity of a structure increases with the amount of "origami paper" that gets folded up to construct it. This complexity, or entropy, may have physical significance. Gravitational entropy could be related to the mystery of "dark energy," the puzzling increasing expansion rate of the universe. The so-called "coincidence problem" is this: why is the acceleration of the universe turning on roughly now, and not say 10 billion years ago or 10 billion years in the future? A speculative answer is that the complexity in the universe has to reach a certain threshold before acceleration can turn on. On astronomical timescales, humans have also come to sentience just when the Universe has reached this level of complexity.
This study of complexity will be a major part of a Templeton Foundation New Frontiers in Astronomy & Cosmology grant that I was awarded last month, along with my colleague, Dr. Miguel Aragón-Calvo. Along with doing cutting-edge cosmology and cosmic-web research, he is at the very forefront of scientific visualizations, for example winning last year's National Science Foundation International Science & Engineering Visualization Challenge with his cosmic-web poster. We are both assistant research scientists in the Institute for Data-Intensive Engineering and Science (IDIES), led by Director Alex Szalay, and in the Physics and Astronomy Department at Johns Hopkins University.
For more information, visit Mark's website.
Download and print the galaxy crease patterns here!
And please visit Eric Gjerde's website, where several "origami tessellations" that happen to be related to cosmological origami can be found.
