In forensic accounting, if you think a company might be messing around with the numbers, there is a math trick you can use as a quick sanity-check, and to find anomalies in the transactions a company gives you. It's called Benford's Law, or the First-Digit-Law.
You might think that in a random group of numbers, there would be just as many numbers that start with a one as start with any other digit. So, if we had a group of nine-hundred numbers, one-hundred would start with a "1", one-hundred would start with a "2" going all the way up to one-hundred starting with a "9."
However, in 1937, Frank Benford wrote a paper titled "The Law of Anomalous Numbers" in the Proceedings of the American Philosophical Society. Benford was an electrical engineer and physicist who spent thirty-eight years working as a researcher for General Electric. In the paper, he proved mathematically that our intuition about these numbers was completely wrong.
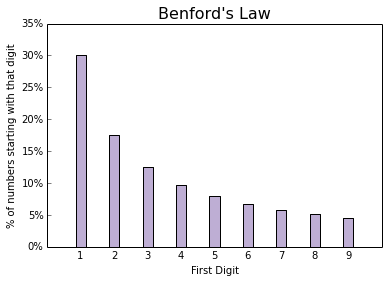
Benford's discovery was that in a large group of numbers, we actually expect more numbers to start with "1" than start with "2", and more numbers to start with "2" than with "3", all the way up to "9." Specifically, in a large group of numbers, we would expect 30.1% of the numbers to start with "1", and only 4.6% to start with "9." The expected distribution for all digits, now known as Benford's Law, can be found in the graph below:
So what happens when a group of numbers doesn't seem to fit with Benford's Law? You've found an anomaly and need to investigate!
Sometimes there's an obvious explanation for why a group of numbers doesn't satisfy Benford's Law. If we looked at transactions from the Queens-Midtown Tunnel, the first digits wouldn't follow Benford's Law, because the toll is $7.50, so most of the transactions probably start with a "7."
Sometimes, when a group of numbers doesn't conform to Benford's Law, it's because someone is cooking the books. Most people don't know about Benford's Law, so when they make up fake transactions, they distribute those fake transactions uniformly across all nine digits to make them blend in. Their effort to hide these transactions causes them to put too many transactions starting with nines, not enough starting with ones, and get caught by Benford's Law.
Now let's take Benford's Law and apply it to the US Budget to see if everything checks out!
First we need to gather the data, which is typically the most challenging part of working with government data. Once we have the data, running the Benford analysis is simple.
The US Government is such a massive and distributed organization that collecting the data individually from each government agency might take years. Luckily, in the last budget proposal, the White House attached a spreadsheet showing the line items in the federal budget for the last thirty-seven years. I previously used this data to create an interactive visualization of the US Budget, and we can now use it to check if it conforms to Benford's Law.
This data doesn't include every single government expense, but it should be enough for our purposes. It's a three-level deep summary of the US Budget, with 4,301 individual line items over thirty-seven years, for a total of 159,137 data points.
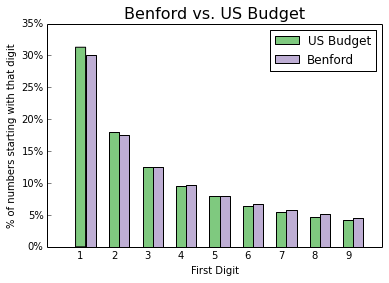
So now, let's take that data, and see how it compares to what we would expect under Benford's Law.
Looks like expenses in the federal budget conform to Benford's Law.
Phew! This may be the first time there has ever been an analysis of the US Budget using Benford's Law, and if the data didn't conform, we might all be in a lot of trouble.