
All over the world youth moan and groan when their math calculations are off and celebrate, often accentuated with a fist pump, when they're right. It's happening right now. In a class? Possibly, but much more frequently on a bus, subway, car, or in doctor's office. It's a craze. Children, youth, and adults wear Halloween costumes, winter hats, and T-shirts related to this application of math. Sound impossible? Not at all. Simply play the popular video game Angry Birds, and every time you prepare to launch an incensed bird through the air, you are using math.
On a smartphone or tablet, or through your browser, let's play Angry Birds. Each launch of a bird from the slingshot with the intent of a collision with a pig or fortified structure requires you to estimate a path of flight. Let's play with a bit of a different goal, in part, so you look at the game in a new way, especially if you are an avid player.

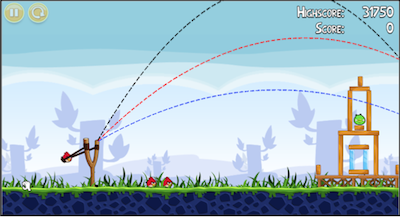
Looking at the screenshot above, how would you launch the bird so that it lands in front of the tower without hitting anything but the ground? Keep in mind that every time you change the launch angle for the bird, you are predicting its path. Now, launch the bird. Did you foresee the bounce? How close was the actual trajectory to your predicted one? Note the puffs of smoke that mark the path; they follow a nice smooth curve. Physicist Dr. Rhett Allain studied the game and verified in his article The Physics of Angry Birds that our feathered friends travel without air resistance. So, a bird's path is a parabola.
Mathematically, parabolas can be written as y = ax² + bx + c. Choosing specific values for a, b, and c defines a curve. In Angry Birds, if you find the right a, b, and c, the birds enact their revenge on the pigs and their fortresses.
Can our knowledge of parabolas yield other information about this popular game? To begin, we must define a scale that can be consistent from screen to screen. We'll use a scale of 1 slingshot and adapt Dr. Allian's notation and write it as 1 AB, as seen below.
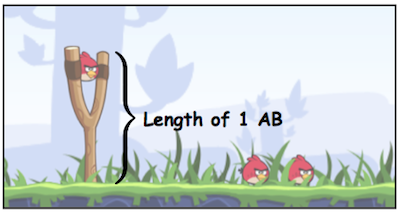
A parabola, in the absence of air resistance, is also defined by an initial velocity and angle of launch. The birds are launched one unit above the ground. So, their initial point is (0,1). Adapting Allian's research, the parabolas can be derived for different decisions. Consider three different launch angles of 30, 45, and 60 degrees; we get:
Below, we see the curves for a bird slung at these angles. We see that for this screen only a 30-degree shot will result in an air strike.
What height will a bird be when it crosses the vertical line seen below if shot at 45 degrees? To answer this, we must determine where the dotted line crosses our x-axis.

Remember, 1 unit = the height of a slingshot. If we lay slingshots down one after another, we see that the dotted line is 5 units from the launching spot. So, we need only to set x = 5 in the formula y = 1 + x - 0.106x² = 1 + 5 - 0106(25) = 3.35. In the picture below, we see the projected height of the bird when it crosses the dotted line. Good enough for an arial view of the pig's fortress.

When you play Angry Birds, you visually estimate the coordinates of your target and use this to determine your initial angle. In North Carolina Kristianna Luce motivates topics of Algebra 1 using Angry Birds, which was a connection introduced in my Charlotte Teachers Institute seminar Math Through Pop Culture.
To begin, Luce had her students play the game, much as we did to begin this article. Soon, she directed the conversation toward asking what would be the highest point for a bird. Such a point is called vertex of the parabola. Given our work here, let's find the highest point for a bird launched at 60 degrees. This occurs at x = -b/2a. For 60 degrees, a trajectory follows y = 1 + 1.732x - 0.211x². So, a = -0.211 and b = 1.732. The vertex occurs at x = 1.732/(0.411) = 4.214 at a height equalling 1 + 1.732(4.214) - 0.211(4.214)² = 4.552. Note from the picture above that the top of the initial screen is about 4 slingshots high.
Luce's students used their knowledge of Angry Birds to help with algebra problems on their end-of-course exams. We'll consider two sample problems released by the North Carolina Department of Public Instruction. One question asks for the roots of the equation 0 = 9x² - 49. What would this be asking in the context of birds and pigs? Luce's class had discussed the point where a bird hits the ground; this is a root of the parabola and can be found using the quadratic formula. Our problem corresponds to an angry bird following the path y = 9x² - 49 and requires finding the points where this curve hits the ground, with a point existing on either side of the slingshot. Another sample end-of-course problem asks for approximate solutions to the equation x² + 4x = -2. Here a bird follows the trajectory y = x² + 4x, and we are interested in the x coordinate when the bird is 2 units below the ground.
We use math every day. In fact, given the mathematical thinking required in Angry Birds, math is used a lot every day! Further, Angry Birds can help in math class. Frustrated with math? Play Angry Birds and remember math and its application can be fun.
