
Thinking about food can sometimes lead to artistic and mathematical insight. As with many things in life, especially those involving taste or sight, it's all a matter of proportion and balance.

Vermeer's "The Music Lesson" (c. 1665)
Last time around we upset the orange cart to make some points about scaling, in dimensions familiar and not so familiar. Below, we embark on additional (and subtractional) fruitful explorations, which also encourage us to expand our horizons a little.
We start by considering an elementary ratio principle whose geometric underpinning has been used to add realism to art for centuries, and today gives computer animations a boost in two unrelated ways. We introduce it as a kind of proportional representation for flavor, but it applies equally well in many other gastronomic and graphic contexts. If readers get stuck with any of the technical details below, they should feel free to skip ahead and pick up the thread again later. (That simple advice should always be followed by readers young and old and in between, of any level mathematics, in any context!)
Balancing Act
Suppose we wish to make a smoothie, from two available ingredients: Apple and Blueberry purees. While the question of the perfect balance of flavors is a highly personal one, at least we can describe all of the possibilities dispassionately, using elementary mathematics. It's a little trickier if we also have Cranberry puree at our disposal.



3D glasses
Obviously a recipe recommending eight parts Apple to four parts Blueberry yields the same mix as the simpler one asking for two parts Apple to one part Blueberry. But what about nine parts Apple and four parts Blueberry?
We coordinate these Apple/Blueberry possibilities with pairs (A,B) = (8,4), (2,1) and (9,4) respectively. The first two smoothies are indistinguishable since they have the same A/B ratios, namely, 8/4 = 2/1 = 2, and hence the same flavor. Less sophisticated taste buds may have trouble telling those apart from the third possibility, since 9/4 = 2.25.
Those not so keen on Blueberry may desire an Apple intensive (8,1) with ratio 8/1 = 8, and those preferring almost no Apple may opt for a Blueberry blitz such as (1,10) with an A/B ratio of 1/10 = 0.1. We are of course ignoring actual smoothie quantities, chemistry (possible interactions), and biology (the fact that to our taste buds some flavors naturally dominate others, as grapefruit does over orange). An idealized flavor balance is our only consideration.
To each blend (A,B) we associate a corresponding number A/B. That flavor ratio can vary from small, for blends like (1,10) chosen by die-hard Blueberry lovers, to large, for blends like (8,1) chosen by avid Apple enthusiasts. As mentioned above, we identify (8,4) and (2,1), and likewise write (2,2) = (1,1), with a ratio of 1, for equal parts Apple and Blueberry.
[Those with some exposure to mathematics may realize that, essentially, we are considering points (A,B) in the first quadrant of the associated 2D plane, and identifying all points lying on lines radiating away from the forbidden fruit (0,0); more on that anon.]
What if we cannot abide Apple in any shape or form? Then it's Blueberry all the way: (A,B) = (0,1) with ratio 0/1 = 0, as indicated by the middle blue smoothie image above.
However, an insistence on all Apple all of the time necessitates an unavoidable adjustment: then we have (A,B) = (1,0) with ratio 1/0 = . Note that while is not an ordinary number---and should never be handled by anyone without proper training---there is no danger in using it here. The first green smoothie image above depicts that option; mathematicians know it as the Point (Pint?) at Infinity for a reason that may become obvious shortly. These possible flavor ratios A/B vary continuously from 0 to -- the two extremes of blend loyalty -- with any positive number in between being fair game.
Here's a geometric way to visualize this. Start with a point (A,B) in the first quadrant of the 2D plane, with neither A nor B being negative. Here A measures horizontal distance to the right of the vertical B axis, and B measures vertical distance above the horizontal A axis. Neither axis is drawn below, to avoid clutter, but of course they both go through (0,0). Next consider the horizontal line B = 1 skimming the top of the circle of radius 1 centered at (0,0). Finally, project (A,B) onto this line, meaning locate the point (A/B,1) on it where it meets the diagonal line joining (0,0) to (A,B).
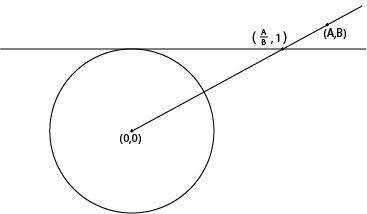
The (A,B) shown in this image is about (2.5,1.25), resulting in the projection (2,1), which should taste familiar from before.
In this way each possible flavor ratio can be viewed as a point on the right half of the horizontal line shown: it's as if we insisted on always using A parts of Apple to 1 part of Blueberry, to get (A,1) with flavor ratio A/1 = A. In this way we can think of A itself varying from 0 to , the final maximally Apple smoothie swamping out the Blueberry totally. Visually that last extreme is "as far out on the right as one can go"---hence the Point at Infinity designation. The diagonal line through (0,0) has in essence become horizontal "in the limit", yet maintains its intersection with the line B = 1!
Note that while above we only mentioned whole numbers and the associated fractions (namely, rational numbers) for A and B, in reality anything goes. Apple for which (A,B) = ( , 1) could be advertized as having more than three times as much Apple as Blueberry. On the other hand, Blueberry for which (A,B) = (1, ) might counterclaim that it has irrationally good flavor. Actually each here can make similar truthful assertions. While is roughly 3.14159 = 314159/100000, it is worth noting that it's an irrational number, meaning that no fraction can ever capture it with full accuracy. Moreover, it also has a certain transcendence quality. The same two assertions are true for its reciprocal 1/.
Projecting Effectively
Mathematicians refer to the above treatment of flavor ratios as the homogeneous coordinate model of the real projective line. There, one studies all pairs (A,B) where A and B are any (positive, zero, or negative) real numbers, only ruling out A = B = 0. The upshot is that a punctured 2D model -- remember we left out (0,0) -- has been reduced to an augmented 1D one.
The smoothie model above also insisted that A and B are not both zero -- otherwise there would be nothing to drink -- but excluded the negative number possibility. ("It's only a model" -- as Terry Gilliam famously said of a certain castle in Monty Python and the Holy Grail -- but it's a helpful model.)
Now let's throw Cranberry puree into the mix. Consider all triples (A,B,C), where not all three are zero, sensibly agreeing that (2,3,1) = (4,6,2), and (3,3,3) = (1,1,1). The smoothie (2,1,0) we've already met above, whereas (0,1,5) is for Cranberry lovers who don't mind a little Blueberry, but shun all Apple.
Visualizing this model geometrically requires looking at points (A,B,C) in 3D and identifying all points which lie on lines radiating from the center (0,0,0). Another way of viewing at this is to assume that we always use A parts Apple, B parts Blueberry, and 1 part Cranberry, to get (A,B,1), with A and B both varying from 0 to ∞. Provided that C isn't zero, any (A,B,C) thus yields a special flavor (A/C,B/C,1) on the horizontal plane C = 1.
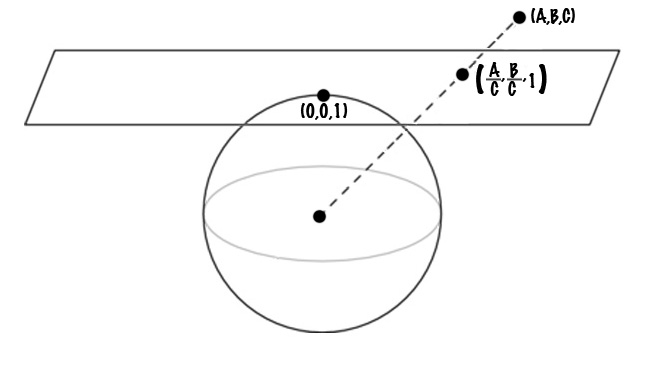
The implicit A and B axes here lie on another horizontal floor plane parallel to the one shown, only passing through the center of the sphere. The equally-invisible vertical C axis also goes through the center (0,0,0) of the sphere, and measures distance above the floor C = 0.
What if C = 0 for a flavor (A,B,C)? Well, on the one hand we've already been there and done that, and in some detail: it's the world of Apple/Blueberry blends. In this 3D geometric model, however, we have something like the oft-sampled (2,1,0) which can now be thought of as one of an infinite number of Points at Infinity lying on a head-spinning Line (or Circle) at Infinity on the extended floor.
There is one such Point at Infinity for each and every Cranberry-avoiding smoothie blend, namely each direction through (0,0) in the 2D world (including the "horizontal one" that gave us a little trouble there). These points are where parallel lines in the plane meet! (Renzo Cavalieri of Colorado State University has a nice explanation of that unlikely-sounding but unavoidable scenario here). One could argue that these Points at Infinity are out at the extreme edges of the horizontal plane shown above, just as the sole Point at Infinity earlier was out at the extreme right (and left, did we mention that?) of the horizontal line in the previous image.
What we have here is a punctured 3D model which has been reduced to an augmented 2D one: a horizontal plane and a bounding infinite circle. Mathematicians know this as the real projective plane.
Additional flavors can be accommodated by adding more coordinates in higher dimensions. A smoothie made using some of four available flavors---anybody for a dash of Durian?---can be modeled by stepping into 4D space and considering (A,B,C,D), not all zero. This in turn can be brought back to a 3D world augmented by a "sphere at infinity." Add Elderberry to the mix, and we'd have to start in 5D space and then back to an augmented 4D world.
Whoever said higher dimensions were unimaginable and impractical? You may have trouble visualizing them, but you can certainly taste the results. Perhaps a balance of the five (or is it six?) basic components of taste can also be analyzed in augmented 4D or 5D worlds, although there is not yet umaminous agreement on this point .
Primary Sources
What we have considered above for flavor blending is well known for color blending in two distinct but complementary situations: light and paint mixing. A Field Guide to Digital Color by Maureen Stone (A.K. Peters, 2003) is a terrific printed resource for those desiring comprehensive information. Here we merely sketch the basic highlights.
The three smoothies which we showed above have bright colors which are closer to the additive primary colors Red, Green, and Blue, than the appearance of true fruit purees.



RGB Smoothies
The additive color model is suitable for explaining how color is produced on a digital display screen, or less technologically by shining three lights on a white wall, one of each true additive primary color, in varying intensities, to produce any desired shade.
For instance, full intensity combinations of any two of those primaries yield three other key colors: Green and Red give Yellow; Green and Blue give a pale blue known as Cyan (or aqua); and Red and Blue give a kind of purple known as Magenta (or fuchsia).



CMY Smoothies
In the RGB model, if all three lights are used in equal intensities some shade of gray is obtained, ranging from black (zero intensity) to white (full blast). Hence, triples (R,G.B) with the same coordinates vary from black = (0,0,0) to white = (1,1,1), with (0.5,0.5,0,5) being a mid-level gray. Note that this is not a homogeneous coordinate model per se. Similarly, (1,0,1) denotes Magenta, and (0.5,0.0.5) is a duller version of that akin to purple.
On the other hand, in any environment where reflected light is key, such as adding color paint or dye to a white base, or ink for printing on white paper, the complementary CMY subtractive primary colors Cyan, Magenta, and Yellow are the building blocks of color. (Can you guess what colors are obtained when two of those are combined in equal intensity? Yes, there is a duality at play here.)
It's not the way artists necessarily think of color mixing when some primary sources (e.g., cobalt) are very expensive, but it is a valid way to mix. It's certainly how most laser printers work today, throwing in Black too as a fourth ink, it being the most commonly used color.
Long before the digital era, color photography used the subtractive model (printing the results on paper); amazingly it goes back at least as far as the work of Louis Arthur Ducos du Hauron in 1867.
Unparalleled Improvements
For six centuries, what we now know as projective geometry has played another role in how humans represent the 3D world around us on a 2D canvas, and hence more recently how computer graphics represents 3D scenes on 2D screens. The C = 1 plane astride the sphere earlier was crudely rendered. The image below on the left, from our last romp here, is also overly simplistic, and lacks reality:

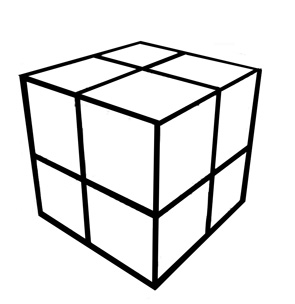
It's all a matter of perspective: the problem here is that opposite sides of the cube, which are parallel in real life, actually look parallel in the left image! The image on the right is better, even if it overcompensates a little, but it does illustrate foreshortening, and the all-important vanishing points on an imaginary horizon (where, you guessed it, parallel lines meet).
Addressing these issues took time in Western drawing and painting. Giotto di Bondone's "Christ before Caiaphas" (c. 1305) on the left below is considered a step in the right direction in this realm.


However, Simon Ushakov's well-though-of "Last Supper" (1685) from almost three centuries later, shows little progress by comparison.
David Henderson and Daina Taimina, in their groundbreaking book Experiencing Geometry: Euclidean and non-Euclidean with History (Prentice Hall, 2005) remind us that projective geometry had its origins in Euclid's Optics (circa 300 BCE), and they also credit the earliest documented use of mathematical rules for getting correct perspective in art to Optics aficionado Filippo Brunelleshi around 1413.
By the 1660s, Johannes Vermeer, the would-be photorealist of his era, had already got all of this so squared away, e.g., in The Music Lesson (shown at the very top of this article, far above) and Girl Reading a Letter by an Open Window, that a full 3D reconstruction of the latter was recently shown to be possible.
Graphic Acceleration
Computer graphics has learnt those lessons well, and uses the same principles to give a 3D impression on a 2D screen, not only statically, but also dynamically in the form of video and special effects.
But there is another, less well known, but really important role that homogeneous coordinates and projective geometry play in fast-moving digital graphics. It's a bit technical so we'll make it fairly brief.
Two of the most basic types of motion one needs to depict on screen are straight line (translations) and spinning (rotations). The latter is easy to effect on a computer thanks to the use of 3 by 3 matrices (think tiny spreadsheets where all entries are numbers). Numerical software has long been optimized to combine vast numbers of matrices (using multiplication) in very little time, which is necessary for the real time rendering of rapidly moving objects in animations and special effects. Translations, however, cannot be implemented directly in this way.
The workaround is to take the desired 3D world and add an extra dimension by "homogenizing coordinates to 4D". In this enlarged world rotations are still matrix multiplications, and, magically, so are translations. Even better, perspective projection can be handled in this way too. It's all done with lightning speed by software using 4 by 4 matrices. The results are "projected" back down to 3D; and in due course, thanks to the projective geometry of perspective, to the 2D screens which fool the human eye. Few viewers have any idea how much clever mathematics is at work backstage.
All of which goes to show, once again, that it's often a good idea to think outside the box.
These days, printing isn't restricted to 2D either of course. Evelyn Lamb has a nice Scientific American piece on Saul Schleimer and Henry Segerman's amazing 3D printing of 4D objects.
We sign off with an appealing incarnation of the spirit of Piet Mondrian, an abstract artist who was fond of vertical and horizontal lines as well as primary colors, courtesy of its creator Louis Davidson of http://www.davidsondigital.net.

Tempting though it is to think of the lines depicted on the apple as straight, most of them aren't; but that's a story for another day.
For graphics production and assistance, thanks to Spelman College's Dan Bascelli, and also to Henry Peteet. Scott Anderson and Barbara Nesin provided some graphics and artistic fact checking, respectively. Arty opinions expressed are the responsibility of the author. All images used with permission.