Is it possible to arrange 20 infinitely long cigarettes in such a way that each one touches the other 19? No bending or breaking is allowed. Cutting off the unneeded ends--away from the zones where cigarettes touch--we'd have finite cigarettes (of the same length, if desired) which could be packaged up and sold as unique keepsakes. No smoke, no fire.
Mathematicians (and perhaps engineers) would really like to know if it can be done. Two years ago a modest breakthrough was made in this quest, after it was shown that it works for seven infinite cigarettes (or cylinders), settling an issue raised 45 years before that.
CAPTION: One realization of seven (potentially) infinite mutually touching cylinders (by Bozóki, Lee & Rónyai, 2013). Photo by Colm Mulcahy
One person who'd like to know the answer, if he were alive, would be influential and prolific writer Martin Gardner (1914-2010). This Wednesday marks the 101st anniversary of his birth in Tusla, Oklahoma. (My Google Tech Talk Martin Gardner 101 surveys his legacy.) His 80-year long publishing career began in the spring of 1930, with a magic trick called "Color Divination" in the Sphinx magazine, and within five years he had released Match-ic: More than Seventy Impromptu Tricks with Matches (Ireland Magic, 1935), the first of seven magic pamphlets that he authored between 1935 and 1949.

CAPTION: Martin Gardner takes a well earned break in 2006, having written all of the books on the shelves. By the time he died, in 2010, he'd authored 101 non-fiction books alone. (Photo credit: Colm Mulcahy)
In the mid 1950s, he wrote Mathematics, Magic and Mystery (Dover, 1956), still in print and still a classic. Its magical items use paper, rubber bands, dice, cards and other low-tech props to amaze and amuse, minus any sleight of hand. By 1960 his career had veered into science and mathematics journalism--he was also a pioneering rationalist and skeptic--and he was well established as a popular and influential columnist for Scientific American magazine, a position he maintained well into the 1980s. He'd also published his best selling book on Alice in Wonderland, which has just been reissued as The Annotated Alice: 150th Anniversary Deluxe Edition (W.W Norton), a final updating that incorporates notes he left when he died five years ago.
Recreational mathematics is what Martin is probably best remembered for, as recently highlighted in the New York Times by mathematician and novelist Manil Suri. NPR's "Math Guy" Keith Devlin and MacArthur prize winner Persi Diaconis are among those big names who have heaped praise on Martin's legacy, style and reach. Others are John H. Conway, Rudy Rucker, Don Knuth and Isaac Asimov. His forte was allowing his readers to have their own precious"Aha!" moments, in a pre-internet era when answers to conundrums were not easily found without trying the problem for oneself.
"Googling is not the Gardner way. The Gardner way is to ignite your fascination so that you experience the pleasure of finding the answer yourself."-- Bob Crease in Physics World (October 2014)
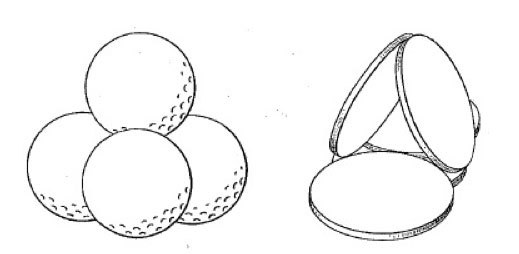
In November 1957, in Scientific American, Martin pointed out (with matching illustrations, as below) that "Four golf balls can be placed so that each ball touches the other three. Five half-dollars can be arranged so that each coin touches the other four."
He then asked, "Is it possible to place six cigarettes so that each touches the other five? The cigarettes must not be bent or broken." (A healthier and equivalent alternative is to consider mutually touching cylinders such as pencils, straws, or pieces of chalk.) What he had in mind was the solution below, in which the hexagonal cross-sections of the pencils shown play no role.

He was pleasantly surprised when some readers showed how to go one step further and have seven mutually touching cylinders! Can you come up with such an arrangement? Like the picture above, the solution he was sent took full advantage of the facts that the cylinders depicted have ends. But what if they don't?
In 1968, English mathematician J.E. Littlewood (of Hardy & Littlewood fame) asked if seven infinite cigarettes could be arranged so that each touches all the others. The breakthrough came in 2013, when Sándor Bozóki, Tsung-Lin Lee & Lajos Rónyai showed that the answer was yes! Some technical details can be found here, and more mathematical background is here.
In March 2014, some of them traveled to Atlanta to present their findings at a Gathering for Gardner--the by-invitation-only bi-annual conferences which focus on extending the legacy of Martin in mathematics, magic, rationality, and so on. They showed off physical models of the two solutions they'd found using a combination of mathematical cleverness, computer power, and careful checking. The models were necessarily truncated in length--thereby avoiding any embarrassing encounters with TSA--and looked like they were assembled using pieces of brightly colored chalk. One of them was shown at the top above; here's the other:
CAPTION: Another realization of seven (potentially) infinite mutually touching cigarettes (by Bozóki, Lee & Rónyai, 2013). Photo by Colm Mulcahy
It's natural now to ask if it's possible to arrange eight infinite cigarettes so that each touches all the others? So far, nobody can say. Amazingly all we know for sure (thanks to A. Bezdek, 2005) is that this can't be done for more than 24 infinite cigarettes!
So at present we can't rule out the existence of a special packet of 20 cigarettes thoughtfully arranged so that each touches all of the others without using the ends of the cigarettes to make contact. All we can rule out is a 25-pack. In fact, we'd be thrilled to just have an eight-pack with the desired property. There are surely potential engineering implications too.
We just don't know what the mathematically optimal pack of cigarettes of this type is, in other words how many infinite cylinders can be accommodated. One with eight, nine, or maybe a lot more? Or must we settle for seven as shown above? It's too early to say, it seems. This burning issue remains unresolved for now.
This is just one example of people continuing to push the envelope by chipping away at (or extending) old problems which Martin first introduced to his huge reader base--it's said he had a million readers each month in his Scientific American heyday. Another example is this summer's surprising discovery by a team at the University of Washington Bothell of a previously unknown way to fit together infinitely many copies of a special type of pentagon to fill up the plane, as discussed here at Huffington Post by David Freeman.
Take another look at the two pictures of seven (potentially) infinite mutually touching cylinders above. Don't they look like seven pieces of chalk grabbed awkwardly from a box, in one hand, and held aloft? Isn't it more than possible that somebody--a child perhaps--has held up such an arrangement of pencils or straws at some point in the last century, oblivious to the significance of the gesture? Likewise, maybe such an event has occurred with more than eight cylinders in one hand, all touching each other. If it did, nobody noticed. It's strange that mathematics can help to land men on the moon and keep us all connected in this digital age, but can't get a handle on this seemingly much simpler problem.
CAPTION: A 2014 Celebration of Mind at MoMath, New York, NY.
Those curious about the fun-loving and exploratory philosophy of Martin Gardner should attend (or host) a Celebration of Mind at this time of year. Learn more by watching this 2 minute video.
There's still time in 2015, and failing that, please consider next year and beyond, in or around late October. There's no better way to create an environment conducive to having your own satisfying "Aha!" moment.
Colm Mulcahy is Professor of Mathematics at Spelman College in Atlanta, Georgia. He is Chair of the Martin Gardner Centennial Committee, tweets at @CardColm, and suggests that Gardner fans look at the 3 Gardner Twitter feeds.